Vektordatenbanken
- Speicherung und Verwaltung von Vektordaten
- Effiziente Suche nächstgelegener Nachbarn
- Distanzmaße
- Index-Strukturen
- Auch in hochdimensionalen Vektorräumen
- Anwendung in Zusammenhang mit
- Semantischen Vektoreinbettungen (Embeddings)
- Großen Sprachmodellen (Large Language Models, LLM)
- Retrieval Augmented Generation (RAG)
- Aktives Entwicklungsfeld - viele neue Anbieter
Vektoreinbettungen 1
- Vektor = Zahlenfeld fester Länge
- Zweidimensional: (3, 5): Vektor der in der Ebene
- Dreidimensional: (3, 5, 1): Vektor im Raum
- 1536-dimensional: (1.7, 2.9, 0.9, ..., 3.4, 4,7): OpenAI-Texteinbettung
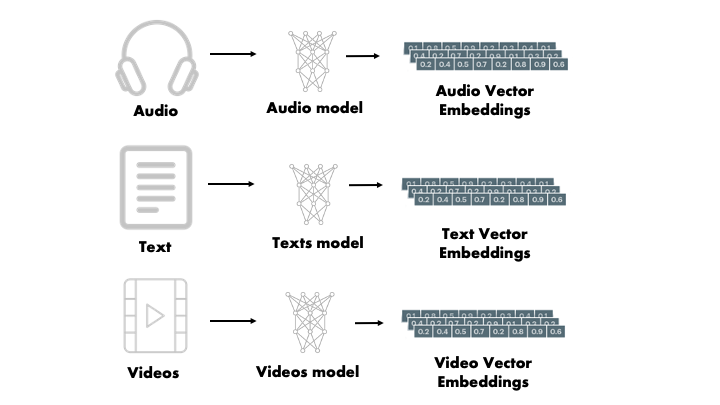
- Einbettungen: Umwandlung von Datenobjekten in Vektoren
- Texte, Bilder, Audio, Video
- Erfassung der Bedeutung der Objekte
- Ähnlichkeiten von Wörtern, Bildern usw.
Vektoreinbettungen 2
- Mathematische Repräsentation von Datenobjekten
- Komprimierte, einheitliche Darstellung
- Bewahren Beziehungen in den Daten
- Ergebnis tiefer neuronaler Netze (Deep Learning)
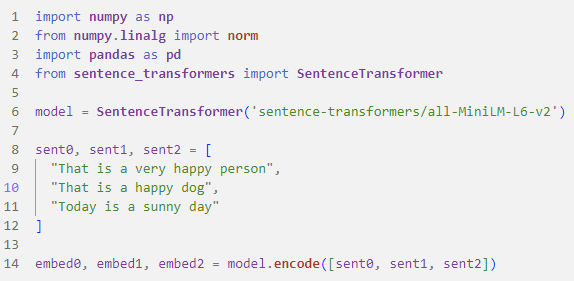
Sentence Transformers

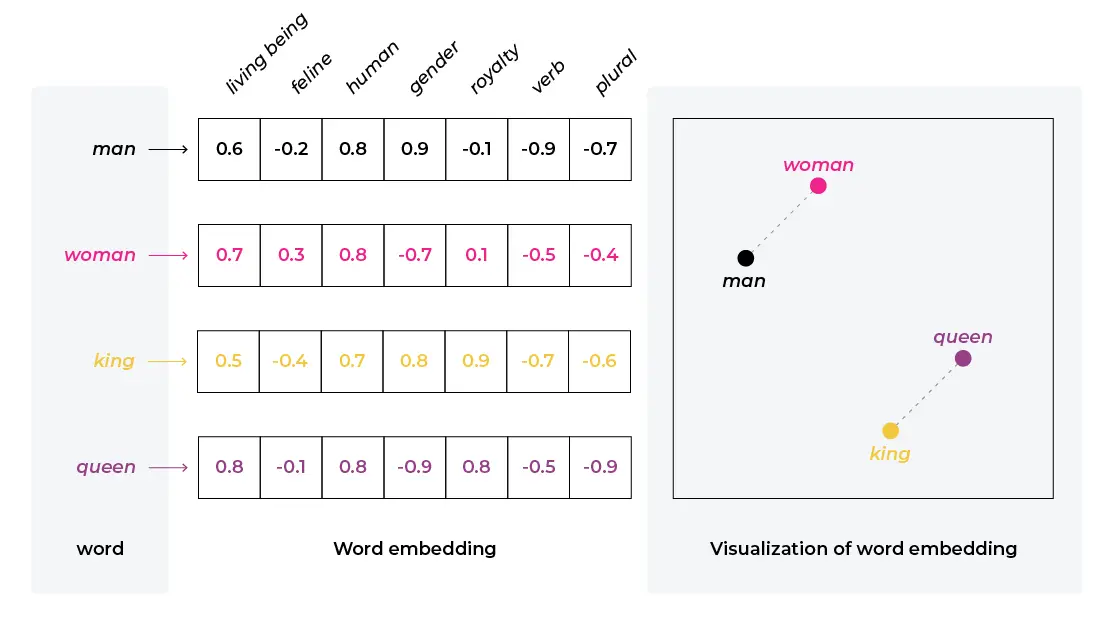
Vektoreinbettungen - Beispiel 1
(Quelle)
Vektoreinbettungen - Beispiel 2

Vektoreinbettungen - Beispiel 3


Explained: Tokens and Embeddings in LLMs (link)
Retrieval Augmented Generation
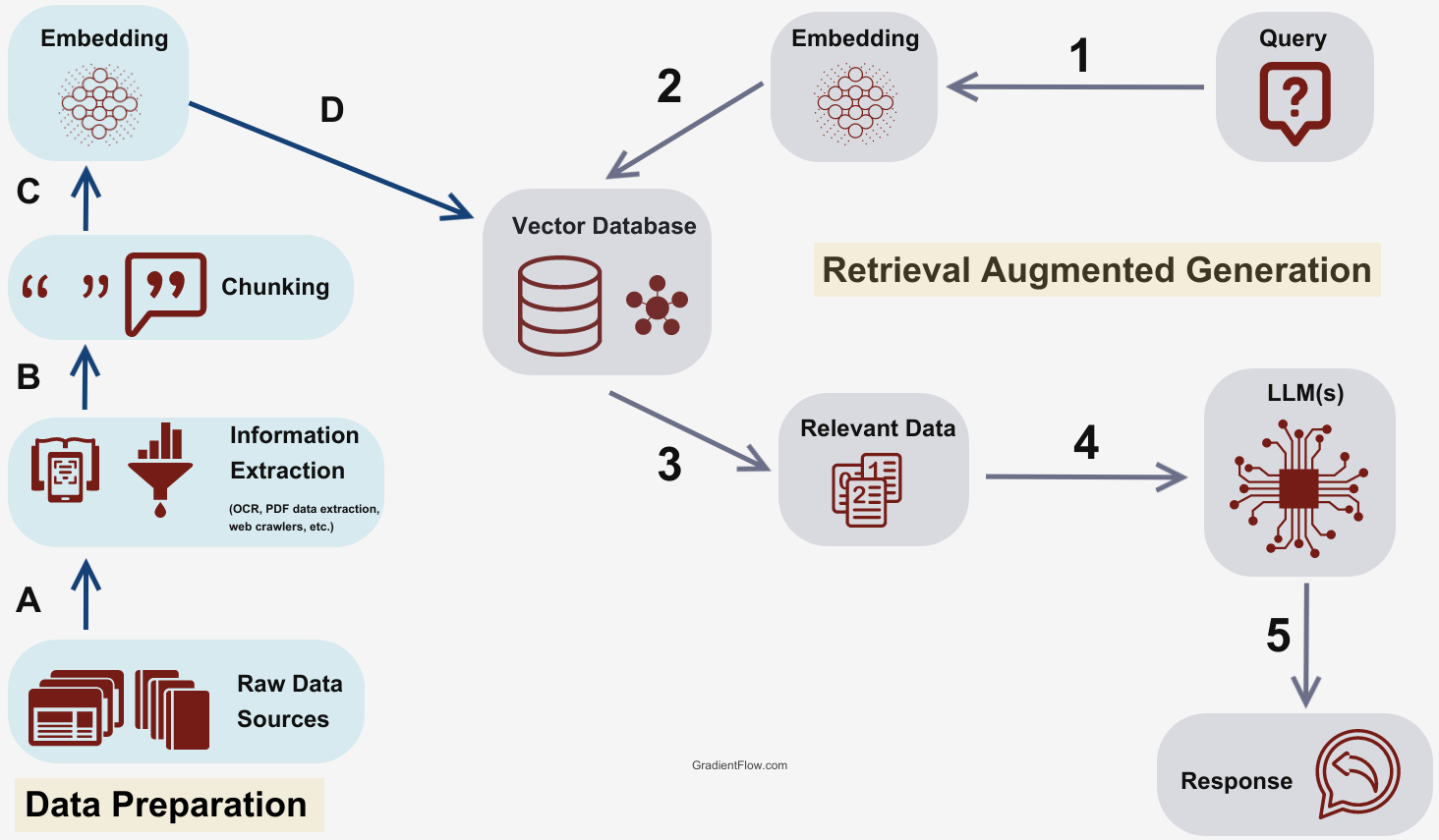
(Quelle)
Distanzmaße

(Quelle)
Gängige Distanzmaße in Vektordatenbanken
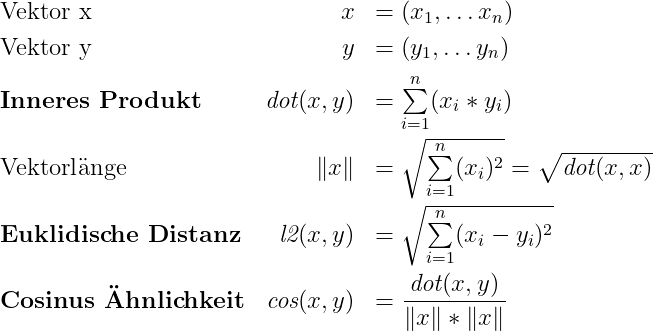
Verteilung im n-dimensionalen Raum 1
Ein-dimensional

Zwei-dimensional
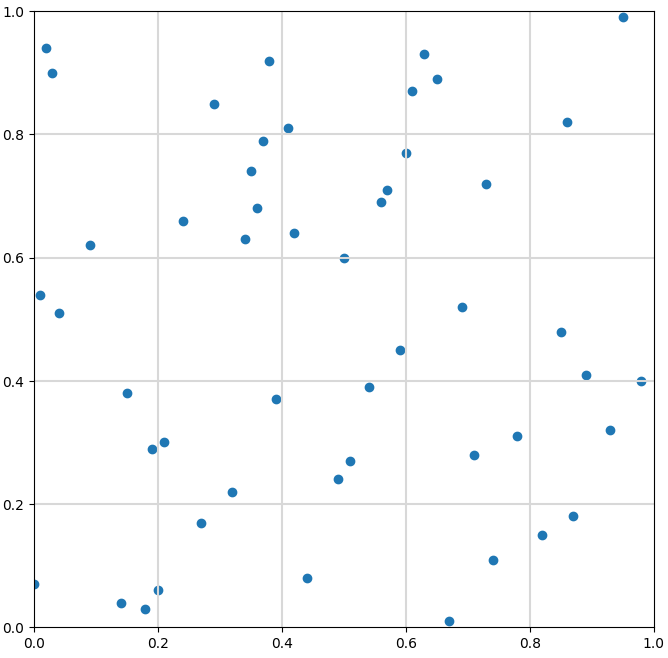
Drei-dimensional

- Verteilung von 50 Datenpunkten
- Seitenlänge eines Teilwürfels: 0.2 Einheiten
- Füllgrad der Teilwürfel nimmt drastisch ab
Verteilung im n-dimensionalen Raum 2
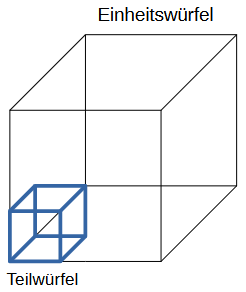
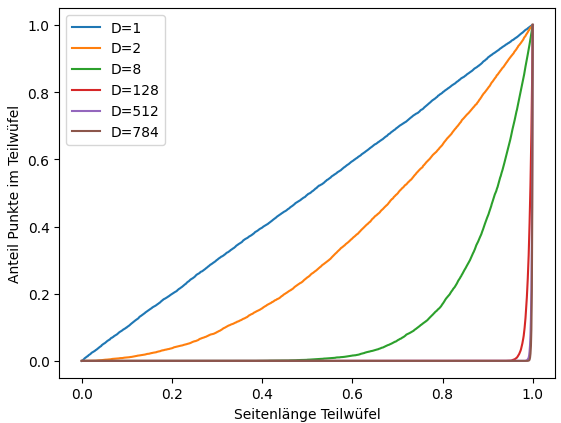
Verhalten der Verteilung bei 20% Seitenlänge
- Ein-dimensional: ca. 20% Datenpunkte
- Zwei-dimensional: ca. 4% Datenpunkte
- Drei-dimensional: viele leere Teilwürfel
- n>10-dimensional: sehr dünn besiedelter Datenraum
784-dimensional: für 20% der Datenpunkte ist über 99,9% Seitenlänge erforderlich
Distanzen im n-dimensinalen Raum

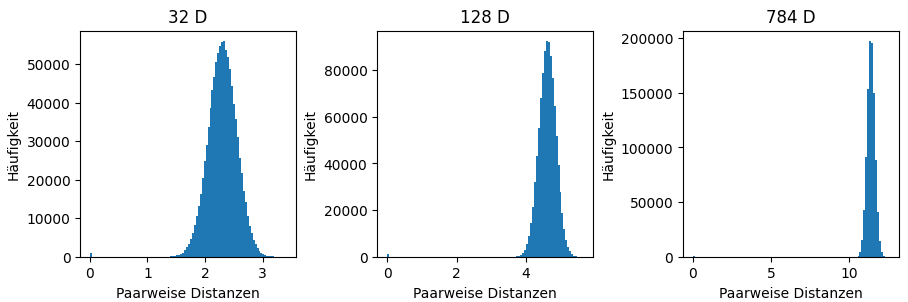
Je mehr Dimensionen, desto
- größer die Abstände
- ähnlicher die Abstände
Fluch der Dimensionalität
Euklidische Distanz verliert an Bedeutung
Vergleich der Ähnlichkeitsmaße
| Cosinus-Ähnlichkeit | Euklidische Distanz | Inneres Prdukt |
|---|---|---|
| Winkel zwischen Vektoren | Abstand zwischen Vektoren | Winkel und Abstand zwischen Vektoren |
| Unabhängigkeit von Größe der Vektoren | Abhängigkeit von Größe der Vektoren | Abhängigkeit von Größe der Vektoren |
Eignung und Einsatzbereiche der jeweiligen Metrik: Untersuchung im Klassenraum
Suchstrategien in Vektordatenbanken
Lineare Suche
- Berechne Distanz des Query-Vektors zu allen Vektoren in der DB
- Liefere Vektor mit geringstem Abstand
- Liefert genaue Ergebnisse
- Zu langsam bei großen Datemengen
Inverted File Index
- Partitionierung des Datenraums auf Basis von Clustering, z.B 256 Cluster
- 256 Zentroide
- Berechne Distanz des Query-Vektors zu allen Zentroiden
- Lineare Suche in der Partition des gefundenen Zentroiden
- Liefert Näherungswerte
- Drastische Reduktion der Suchvorgänge
Quantitisierung
- Reduzierung der Genauigkeit der Vektoren
- Spart Speicherplatz, z.B. 8-fach bei float64 zu int8
- Schnellere Abstandsberechnungen auf int8 als auf float64
- Skalare Quantitisierung
- Produkt-Quantitisierung
Hierarchical Navigable Small Worlds (HNSW)
- Umwandlung der Vektoren in einen Graph
- Abstände zwischen Vektoren als Kanten
- Multi-Ebenen-Graph
- Hierarchische Suche im Graphen
Lineare Suche
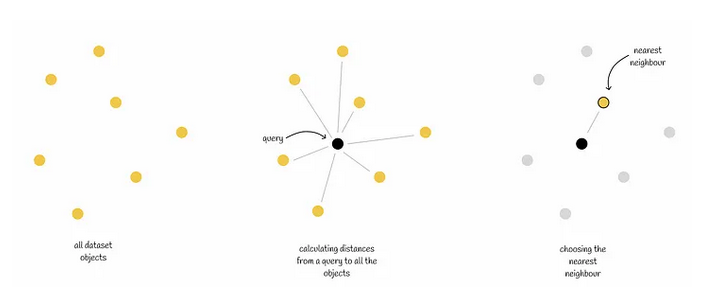
(Quelle)
(Render)
(Download)
Inverted File Index
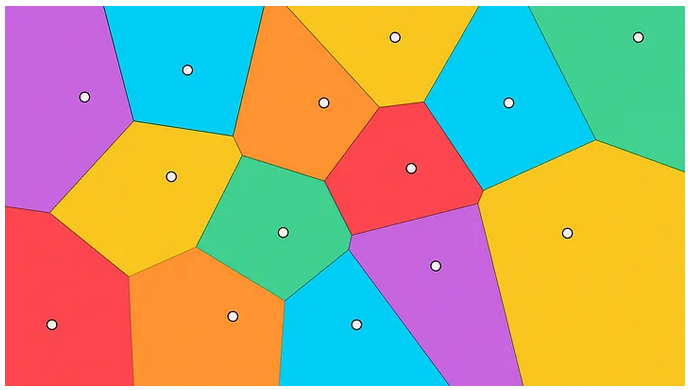
(Quelle)
(Render)
(Download)
Skalare Quantitisierung
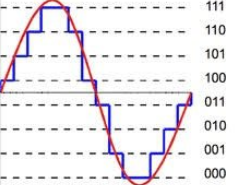
(Quelle)
(Render)
(Download)
Produkt-Quantitisierung
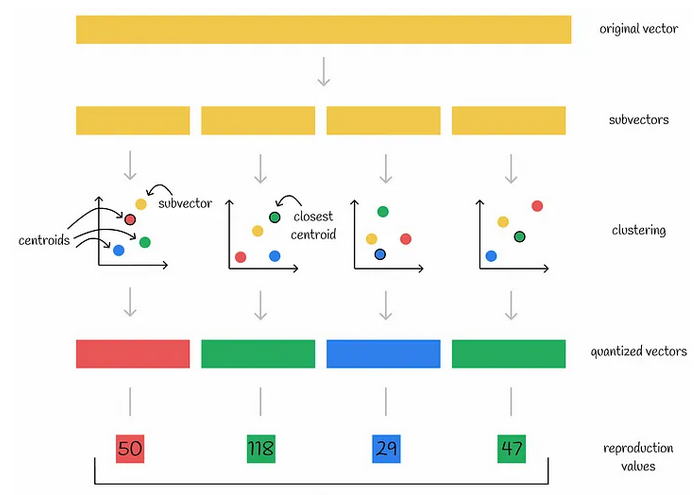
(Quelle)
(Render)
(Download)
Hierarchical Navigable Small Worlds (HNSW)
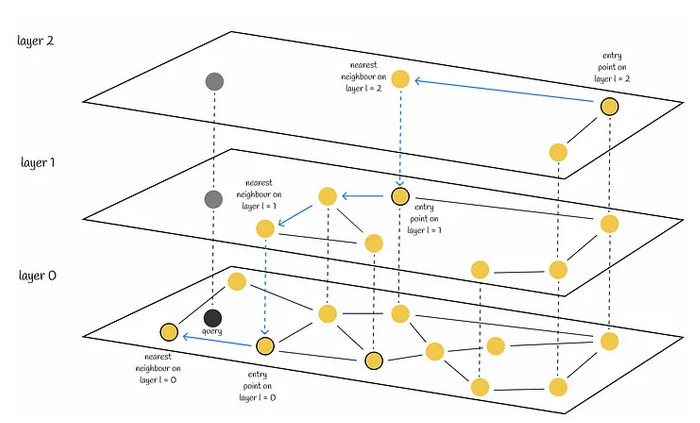
(Quelle)