Rekursive Abfrage - Summierung in einer Hierarchie

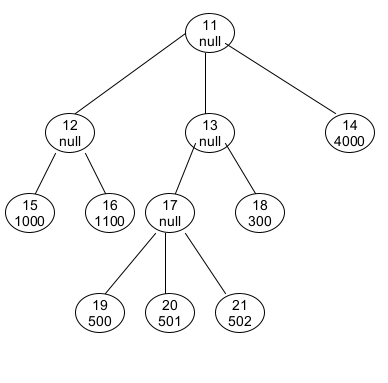
Hierarchie in einer Graphdatenbank

MATCH (x:Node) DETACH DELETE x;

CREATE
  (n11:Node {id: 11}), 
  (n12:Node {id: 12}), 
  (n13:Node {id: 13}), 
  (n14:Node {id: 14, v: 4000}), 
  (n15:Node {id: 15, v: 1000}), 
  (n16:Node {id: 16, v: 1100}), 
  (n17:Node {id: 17}), 
  (n18:Node {id: 18, v: 300}), 
  (n19:Node {id: 19, v: 500}), 
  (n20:Node {id: 20, v: 501}), 
  (n21:Node {id: 21, v: 502})
  
CREATE
  (n12)-[:S]->(n11),
  (n13)-[:S]->(n11),
  (n14)-[:S]->(n11),
  (n15)-[:S]->(n12),
  (n16)-[:S]->(n12),
  (n17)-[:S]->(n13),
  (n18)-[:S]->(n13),
  (n19)-[:S]->(n17),
  (n20)-[:S]->(n17),
  (n21)-[:S]->(n17)

Summierung mit Cypher

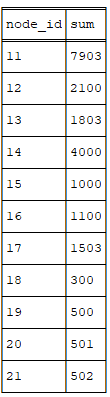
MATCH (p:Node)
OPTIONAL MATCH (c:Node)-[:S*0..]->(p)
WITH p, sum(coalesce(c.v, 0)) AS sum
RETURN p.id AS node_id, sum
ORDER BY node_id

Ergebnis

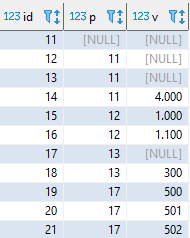
Hierarchie in einer relationalen Datenbank

  create table tree0 (
    id integer not null primary key,
    p integer,
    v integer
  );

  insert into tree0 values (11, null, null);
  insert into tree0 values (12, 11, null);
  insert into tree0 values (13, 11, null);
  insert into tree0 values (14, 11, 4000);
  insert into tree0 values (15, 12, 1000);
  insert into tree0 values (16, 12, 1100);
  insert into tree0 values (17, 13, null);
  insert into tree0 values (18, 13, 300);
  insert into tree0 values (19, 17, 500);
  insert into tree0 values (20, 17, 501);
  insert into tree0 values (21, 17, 502);

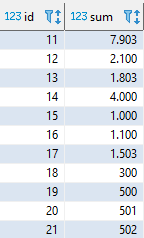
Aufgabenstellung

Schreiben Sie eine SQL-Abfrage, die in einer Baumstrukture alle Werte von den Blättern bis zur Wurzel aufsummiert.

Erwartetes Ergebnis der Abfrage